Chapter 2. Hydrostatics

What you will learn

Understand and assimilate the principles of atmospheric pressure and water pressure
in hydrostatics.

Why

A solid understanding of the pressure characteristics for systems involving water at rest
is an essential requirement in order to understand hydrodynamics.

Duration of chapter 2

1 to 2 hours

2.1. Introduction *

Hydrostatics is the study of the mechanical properties of fluids that are not in motion. In a water
supply system, this is assumed to be the situation at night, when there is no one using the supply
and leaks are insignificant/ignored. Water supply pipes are – and remain - under pressure.

Hydrodynamics will take into account the movement of water through piping systems.

2.2. Pressure *

The pressure is the force per unit area applied in a direction perpendicular to the surface of an
object.
P : Pressure in Pascal [N/m2]
F: Force in Newton [N]
A: Surface in square meters [m2]

Following International System of Units, a pressure of 1 Pascal is created by applying a force of 1
Newton (the force applied by 100g) acting on a plate of 1 square metre. If the same force is applied
on a half square meter plate, the pressure will be doubled (2 Pa). Since a Pascal is quite a small unit, common multiples are more frequently used in practice, as given in the following table. The pressure exerted by a liquid on a surface is directly proportional to its weight; therefore it cannot be negative. Similarly, the pressure exerted by a gas is a function of the impact of its particles against a surface (i.e. a function of its mass and temperature); therefore it cannot be negative.

Different units used for pressure :

The hecto Pascal (hPa) is the unit used in meteorology (1 hPa = 100 Pa)

2.3. Atmospheric pressure

Atmospheric pressure is the force exerted by the weight of air in the Earth's atmosphere. The average pressure at sea level is arbitrarily defined as 1 standard atmosphere (symbol: atm) which is equivalent to 101'325 Pa. An air column of ten square centimeters in cross-section, measured from sea level to the top of the atmosphere, weighs approximately 101.3 Kg.

Atmospheric pressure varies at a given point with the local conditions, (temperature of air, humidity, wind, moon and sun, etc). In the tropics, significant diurnal pressure cycles are observed, this effect
is known as atmospheric tide.

Fig 2- 1 Cyclic variations in atmospheric pressure over two days in Goma

h: height of the liquid column
Pa : atmospheric pressure
p : density of the liquid
g : acceleration due to gravity
A : Section of the tube

When there is no gas (vacuum) in a container, there is no pressure. If we dip the bottom of a test
tube in a bowl of mercury in a complete vacuum, the level of the mercury will remain at the same
level inside the tube and in the bowl (fig 1). If air is then allowed to enter the container, it will push
down on the surface of the mercury in the bowl and a column will rise inside the tube until the
weight of this column counterbalances the air pressure.

To calculate the height of this column, the force due to the air pressure equals the force due to the weight of the mercury column:

 As elevation increases there is less atmospheric mass, so atmospheric pressure decreases with increasing elevation. A simplified relationship (not taking temperature differences into account) is
shown graphically.

P : Mean atmospheric pressure [Pa]
h : Altitude [m]



In this graph, we can see that at 1'000 m above sea level (masl), the mean atmospheric pressure is about 900 hPa (11% less than at sea level); and 750 hPa at 2'500 masl, corresponding to the altitudes in Asmara or Addis Ababa, (25% less than at sea level). In such cases, it might be necessary to take atmospheric pressure into consideration for system design. Min and max pressure depend on location but can be estimated at a first stage at -41 to + 31 hPa from average pressure. The P min has to be used for design, as it is the most critical case.

Fig 2- 2 Variation of pressure with altitude

2.4. Vapour pressure

The vapour pressure is the pressure at which water will vaporise (pass from liquid to vapour). For
instance, at a fixed pressure of 1013 hPa (1atm), water will start to boil at 100 °C and it will remain
at this temperature until it is completely vaporized.
At a constant 20°C, water remains liquid above 24 hPa. However, if the system pressure falls
below this threshold, the water will start to vaporise, producing cavitation (constant temperature,
decrease of pressure).

If water at 20°C is placed in a bowl in a container under vacuum (fig 1), as the pressure is very low,
it will evaporate until the vapour pressure is reached in the container (fig 2). It will then be in a phase equilibrium with two phases, water vapour and liquid water at a pressure of 24 hPa. If the temperature rises, more water will evaporate and the pressure will rise. If the temperature decreases, the vapour will condense and the pressure will decrease. If air at atmospheric pressure is allowed to enter the container (fig 3), a water column will rise in the tube until the column weight balances the pressure differences. While the PV in the container will be included (not added) in the Pa, the Pv in the tube will remain.
In this case, on top of the weight of the water column, you have the vapour pressure, balancing the atmospheric pressure, therefore the Eq 2-2 becomes:

Thus when the temperature rises it will decrease the water column height and when it reaches the boiling point, PV=Pa, the height of the column is zero.
This h gives also the maximum height to which a column of water can be raised or pumped. It will
be about 10 m at 25°C at sea level, but will decrease to about 7.3 m for the same temperature at
2500 m above sea level. For higher temperatures it will decrease quickly, therefore pumping hot
water has to be carefully done.

Fig 2- 3 Vapour pressure in hPa according to temperature

2.5. Relative Water pressure *

The total pressure in the water will be composed of the atmospheric pressure exerted at the
surface of the water plus the pressure due to the water column.

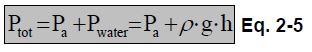Ptot: Total pressure [Pa]
Pa: Atmospheric pressure [Pa]
ρ: water density [kg/m3]
g: is the earth's gravity [m/s2]
h: depth of water [m]

But if we look at the bottom or at the side of a water tank, the atmospheric pressure will act
perpendicular to the surface, counterbalancing the effect of the pressure of the surface of the
water. Thus the pressure on the side and the bottom of a tank will mainly be affected by the depth
(h) of water.
Similarly, when we look at the pressure at the top of a pipe and at the bottom, both are subject to
almost the same atmospheric pressure, therefore the available pressure will be the pressure due to
the difference of water height.

This is why in hydraulics, the pressure (P) refers to the water pressure and not to the total
pressure. This is also why the pressure can under certain conditions be lower than 0 Pa.
For practical reasons, the units used are the bar or the meter of water column:
=> 1 bar ≈ 10 mWC
In a water supply system, pressure can be efficiently created by elevated tanks placed at a high
position. In the following figures the static pressure provided by the elevated tank is 40 mWC or
4 bar

 For house delivery, it is usual to have a pressure ranging from 3 to 5 bars.

The pressure at the bottom of a reservoir is independent of its shape; for the same liquid level (height), the pressure at the bottom will be the same. This is important because in complex piping
systems, it will always be possible to know the pressure at the bottom if the water height is known.

2.6. Archimedes’ principle or buoyancy

Buoyancy is an upward acting force, caused by fluid pressure, which opposes an object's weight.
In hydrostatics, the buoyant force is equal to the weight of fluid displaced by the body.

F: Buoyancy force in Newton [N]
ρ: density of the fluid [Kg/m3]
V: volume of the body [m3]
g: is the earth gravity

This force is always upward (i.e. opposing gravity) as the lateral forces cancel each other out.
If the object is either less dense than the liquid or is shaped appropriately (as in a boat), the force
can keep the object afloat.

Basic exercises

1. What is roughly the pressure an 80kg man exerts on the ground?
2. What is the water pressure at the bottom of a pool 15 m deep at 5°C and at 25°C?

Intermediary exercises

3. What is the average atmospheric pressure at your place and at 4'000 masl?
4. At 4'000 masl, what is the elevation of a column (h) of mercury? and a column of water
according to Eq 2-2?

5. What is the maximum suction height for water at 30°C at 1'500 masl?
6. What is the maximum suction height for water at 15°C at 3'000 masl?
7. What is the buoyant force applied to a body of 2 m3?

Advanced exercises

8. A water pipe has its top at 500 masl and its bottom at sea level. What is the variation of
atmospheric pressure between the top and the bottom? What is the water pressure at the
bottom? What is the ratio between these two pressures?
What is the force applied by the liquid to the side of a water tank that is 2 m high and 10 m
wide?
10. What is the buoyant force exerted on an 80 kg man by the atmosphere (Hint: we suppose
that the density of a man is approximately the same as the one of water)?
11. An air balloon of 1m3 at atmospheric pressure is brought at 10 m below water surface, what
will be the buoyant force? And at 20 m below water surface?